matlab贝叶斯神经网络工具箱|Matlab贝叶斯网工具箱 V2022 最新免费版下载
Matlab贝叶斯网工具箱是一款针对Matlab所推出的神经网络工具。可实现贝叶斯网络结构学习、参数学习、推理和构建贝叶斯分类器等,可支持多种节点(概率分布),精确和近似推理,参数和结构学习,静态和动态模型,免费下载,欢迎体验。
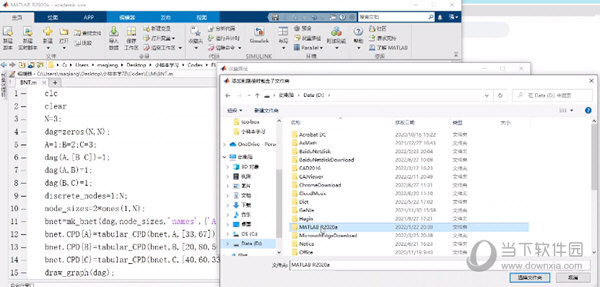
【使用说明】
1引言
在过去十年左右的时间里,已成为一个强大统一的图形化模型形式主义的统计被广泛使用,许多概率模型机学习和工程,范围从混合模型,隐马尔可夫模型(HMMs)的,知识兔从因子分析(PCA):卡尔曼lters。这样做的原因是以下报价描述[Jor99]:
图形模型是概率论与数之间的婚姻图论。他们分享了一个自然的工具用于处理两个问题 发生在整个应用数学和工程不确定性和复杂性,特别是他们发挥越来越在学习机的设计和分析的重要作用算法。根本的图形模型的想法是概念模块化建立一个复杂的系统,结合简单的部分。概率论相结合,使零件的胶,确保该系统作为一个整体是一致的,和分享方式数据接口模型。图论方面的图形模型分享了一个直观的吸引力接口由人类模型高度相互作用的变量集以及数据结构本身自然高效的设计的通用算法。
图形模型缺乏相应的通用软件包。本文介绍了一个企图建立这样一个包,称为贝叶斯网络工具箱(BNT的)。首先,我们将描述图形模型表示,推理和学习的过程中出现的一些问题。然后知识兔,我们将描述现有软件套件的方法,通过对这些问题的。最后,我们描述BNT,它克服了现有的包的一些缺点。
假设读者已经熟悉图形模型的基础:例如,见书[Jor02,CDLS99,Edw00,Jor99,Fre98]。
2概述 图形模型有两种主要的“方式”:直接的和间接的。这也是可以结合定向和无向图。我们将依次讨论每个。
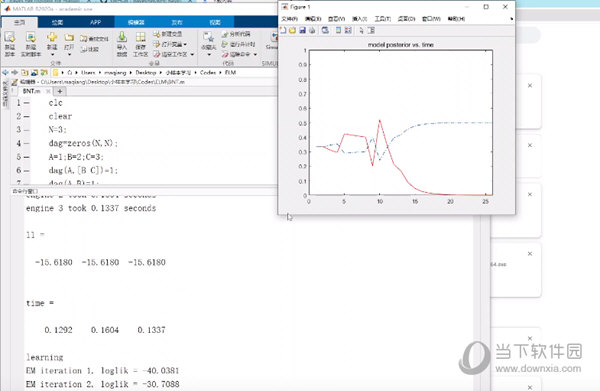
2.1导演的图形模型
向无环图(DAG)的模型,也称为贝叶斯或信仰网络,在人工智能界很受欢迎,部分原因是他们本身的因果解释[Pea00,这使得它们的结构很容易手工设计(如专家系统)。DAG的模型也有用的时空数据建模和动力系统,因为它们可以编码\时间之箭“(这种模式是有时也被称为DBNs,或动态贝叶斯网络。)
DAG的模型也很受欢迎,在贝叶斯统计的社会,因为参数可以明确表示节点(随机变量),并赋予分布(普赖厄斯)。生成的图形,不仅分享了一个简明的规定阳离子模型,但也可以被利用的计算,例如,由Gibbs抽样。这是众所周知的BUGS1包。
一个DAG模型,其中包括决定和实用的节点,知识兔以及机会节点,是被称为一个影响(决定)图,可用于最优决策。
也有一个图形化模型,被称为一个依赖网络[HCM+00]允许执导周期。它可以是有用的数据可视化,但不总是定义一个独特的联合分布:详情请参阅[HCM+00]。
2.1.1定向型号参数
段参数化,知识兔可以定向模型(两个贝叶斯网络和依赖网)通过指定所有本地的条件概率分布(草稿),即,分布P(XijPai),其中Xi表示i节点和排它的父母。最包假设所有节点代表离散的随机变量(分类),另外,除CPDs的是,知识兔可以表示为表
表格的CPDs是简单的代表,学习和使用的推论(见第3.1.1),但缺点是需要的参数是在父母的指数。其他的陈述,只需要一个线性参数的数量,已被提出,知识兔包括嘈杂OR[Pea88]和其概括[MH97],后勤(乙状结肠)函数[Nea92]。
决策树[BFGK96]可以用来表示一个变量(数据依赖)的CPDs参数的数目;他们也有用的变量(母公司)的选择内部结构学习算法(见4.2节)。前馈神经网络(多层感知器,或总纲发展蓝图),条件线性高斯(联络小组)广义线性模型(GLMs)也可以用于连续模式的CPDs节点。
贝叶斯模型,我们需要各种丰富的国家方案文件,例如,Dirichlet先验多项参数,威沙特(伽玛)先验方差/精度参数,知识兔以及为权重矩阵的高斯先验。我们也可以使用非参数分布。
很容易让用户NE异国情调的CPDs。diÆculties出现时,我们希望做相应的模型推断,和/或当我们试图了解参数从数据,我们将讨论下面这些问题。
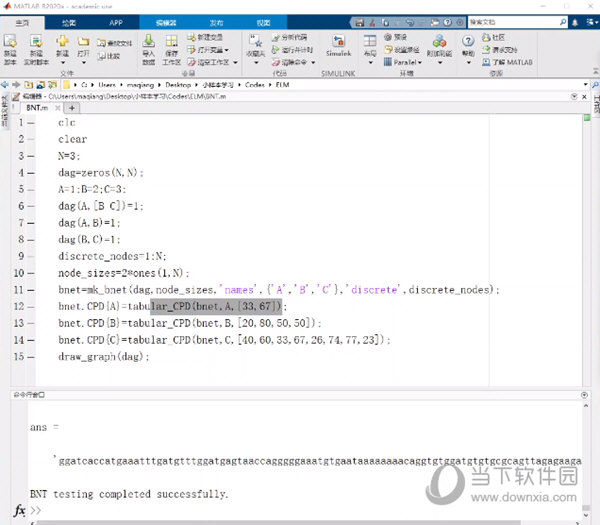
2.2无向图形模式
在无向图形模式,又称马尔可夫网络,共同物理和计算机视觉的社区。对于实例,伊辛模型和马尔可夫随机域(MRFs)电网结构马尔可夫网络。在统计社区,无向模型经常被用来模型多路应急表,在这种情况下,他们被称为(分层)对数线性模型[Edw00]。
2.3混合指示/无向图形模式
它是可以结合到什么叫做链定向和无向图图[CDLS99]一个常见的例子是,在图像处理,其中隐藏节点都连接在一个无向的二维网格,但每个隐藏节点有一个孩子其中包含的像素的观测值(见图1)。至于推论是而言,知识兔可以从隐藏的像素观察表示一个定向或无向弧,但是,有向弧表示首选当谈到学习(见4.1节)。因子图形式主义[KFL01]是一个非常普遍的方式,知识兔使用图形结构在当地代表的全球模型(不一定是概率),或因素。
图1:图像处理链图。每个阴影节点是一个观察像素,是由于其隐藏的父(清);相关的隐患彼此,马尔可夫场与成对潜力随机建模。这是可能间转换[YFW01],尽管所有这些陈述有时信息是“丢失”的过程中从图形结构(此信息将implicitely代表在参数)。这可以等的 计算复杂的推理,知识兔以及模型intrepretability。
3推理
由此推断,我们的意思是计算
其中Xj代表一组观测变量,Xi代表一组隐藏变量的价值,我们估计感兴趣,XK是无关隐藏变量(滋扰)。例如,Xi是否有可能代表疾病我,Xj可能代表观察到的症状。或喜可能代表一个未知参数,Xj的所有数据。有两种主要的推论:精确和近似。我们同时将讨论下面问题。
3.1精确推理
精确推理(有一个封闭的形式解决方案感)是唯一可能一套非常有限的情况下,特别是当所有隐藏节点是离散的,或当所有节点(隐藏和观察)有线性高斯分布(在其中
情况下,网络仅仅是一个稀疏的联合多元高斯参数[SK89,RG99)。专家系统和隐马尔可夫模型(HMMs)属于在前一类,而因子分析和卡尔曼lters的属于后者。
有两种主要的精确推理算法:只有那些工作DAG的模型,和那些定向和无向图的工作。DAG的推理算法利用的规则链的分解合资,P(X) = P(X1)P(X2|X1)P(X3|X1;X2) ….基本上是“推产品内的款项”边缘化无关隐藏的这被称为节点有效[LD94,Dec96,AM00];变量消除算法。计算结果是一个单一的边际P(Xi|Xj)。
一般的推理算法是在消息传递方面的定义上树。如果知识兔原始图无向循环(循环),它必须被转换所谓的交界树使用三角[Kja90]或割集空调[Dra95]。可向或无向树,邮件可通过并行 或连续计算的消息可能会或可能不会涉及除法运算。例如,制定了珍珠的的算法Pea88]有分裂; Hugin/ JLO算法的的定向树[JLO90]制定无向树与分工;和信念传播[YFW01]制定无师无向网络。所有这些算法基本上同等学历。
消息传递算法的优势时问津在计算所有边缘人同时(这是必要的学习,例如):他们用动态规划,知识兔以避免重复计算,将参与调用变量消除了n次,一次为每个变量。然而,变量消除是比较容易实现,使某些优化利用特定查询的知识。
3.1.1电位
实施任何的款项和产品方面的推理算法(例如,变量消除或消息传递),它是要代表每个作为一个对象,它支持的操作(方法)总和/本地分布整合,乘法和可选分工。我们将调用这样一个对象的”潜力”,这仅仅是一个非负的变量在其领域的功能.
如果知识兔在域中的所有随机变量是离散的,我们可以代表一个潜在的作为一个多维数组(表)。如果知识兔在域中的所有随机变量共同高斯,我们可以作为一个多元高斯代表的潜力:简单存储的均值,方差和规模因子。如果知识兔某些变量是离散和一些有高斯,我们可以代表一个条件高斯的潜力(CG),而不是一个标量的表,这是一个高斯表。最后,如果知识兔某些变量是离散随机变量和一些实用变量是离散的,我们可以表示为一对表的潜力;这是在非常有用
uence图。所有这些类型的潜力描述[CDLS99];也见[Mur98b]。
CG潜力可以代表NITE高斯混合物。不幸的是,这表示不关闭。也就是说,如果知识兔我们有一个潜在域(四),其中D是k的可能值的离散变量,C是一个连续变量,PD(四)仍然是一个k个高斯混合:它尚未得到任何小。故重复的款项和产品的应用将导致代表性的大小炸毁。逼近之一是使用\弱边缘化“[Lau92]减少使用矩匹配一个单一的高斯混合高斯模型。(“本实施[Lau92]数值是不稳定的,并已得到改善[LJ99]。)又见Min01]。
无向模型已经参数化潜力,拉帮结派,所以没有转换是必要的。导演模型参数的CPDs 但我们不能简单地定义的潜力∅(Xi;Pai) = P(Xi|Pai)。然而,这是唯一可能的CPDs几种:有关详细信息,请参阅第7.2.1。
抽象层次潜力允许我们重复使用相同的代码许多模型。例如,只需更换与高斯离散潜力相同的代码的潜力,知识兔可以使用,知识兔也可以实现向前向后HMM模型或非线性动力学系统的RTS平滑算法[Mur98a]。
3.2近似推理
即使知识兔在精确推理是数学可能的情况下,它可能不是计算可行的:推理的成本取决于树宽W图(即,规模最大的集团在相应的最佳三角图)。特别是,如果知识兔所有(隐藏)节点是离散的二进制值,推理需要为O(2W)的时间。(联合高斯分布,推论总是在最O(N3),其中n是节点的数目,无论对W;然而,有时(例如,在图像处理中的应用),n是非常大的。)
对于树木(没有无向循环图),树宽是常数(即最大的风扇(父母),图中的任何节点),并推断需要O(n)的时间。然而,对于其他的图形,特别是那些重复结构,树宽电网等,随着变量的数目(例如,在N =毫米网格,树宽是O(M)=(PN)),并准确推断往往是不可行的。
有至少有两个原因之一,可能需要近似推理:要么因为计算精确解时间过长,或因为 是没有封闭形式(分析)解决方案。(精确推理被称为是NP-难一般)。复杂的前一种来自某些种类的图结构,后者由某些种类的分布。(在一般情况下,几乎所有的续随机变量的分布产生棘手的后验,完全观测共轭指数的情况下,是一个值得注意的例外)。下面我们列出一些可以用来处理棘手两种技术。
采样(蒙特卡罗)方法。最简单的一种重要抽样,我们从中随机抽样事先P(x),(无条件)x隐藏变量的分布,然后知识兔重量的样品其的可能性,磷(YJX)的,其中y是证据。一个更多的电子脝cient做法高维被称为蒙特卡罗马尔可夫链(MCMC),这使得我们从后P(XJY)的样品,甚至当我们不能计算正常化常数,接收P(下YJX)P(X)。MCMC方法包括作为特别案件Gibbs抽样的Metropolis-Hasting算法(如见,[Nea93,GRS96,Mac98])。MCMC方法是近似的主要方法在贝叶斯统计推断。变分方法。最简单的例子是坡鹿的平均逼近,利用大数定律随机近似大笔变量的手段。特别是,我们基本上是脱钩的所有节点,并引进一个新的参数,称为变分参数,每个节点,并反复更新这些参数,知识兔以尽量减少近似真实的概率之间的交叉熵(KL距离)分布。更新变参数进行推理成为代理。平均ELD逼近生产下界上的可能性。更复杂的方法是可能的,给予严格的低(上)边界。教程[JGJS98]。最近,这项技术有被延长做近似贝叶斯推理,知识兔使用了
一种叫做变分贝叶斯[GB00]。
信仰的传播(BP)。这就需要采用消息传递算法原始图,即使知识兔它有循环(无向循环)。原本这被认为是不健全的,但优秀的经验成功 [BGT93],这已被证明可以使用BP算法
[MMC98],导致大量的理论分析,这表明了BP是密切相关的变分方法[YFW01,SO01]最近这项技术已延伸到做近似的贝叶斯推理,知识兔使用技术[Min01]称为期望的传播。
下载仅供下载体验和测试学习,不得商用和正当使用。

![PICS3D 2020破解版[免加密]_Crosslight PICS3D 2020(含破解补丁)](/d/p156/2-220420222641552.jpg)